With the
Particle fountain working, now we can finally implement a more complex algorithm for the particle fountain to do gravitational interaction between particles, a type of
N-body simulation.
An N-body simulation simulates forces between N bodies, in this case gravity, though we can apply it to things like fluid dynamics, electromagnetics in particle accelerators etc. In this case, a universe simulation with gravitational interactions is a fun choice.
The most naive approach to N-body simulation is to calculate every single interaction between every single particle, which would be N * N = N^2 calculations, or an O(n^2) solution. This is fine for a small number of particles as the code is at it's simplest here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void calc_all_acc_brute() {
for(int i=0; i<MaxParticles; i++) {
Particle& p = ParticlesContainer[i]; // shortcut
for (int j = i+1; j < MaxParticles; ++j) {
Particle& q = ParticlesContainer[j]; // shortcut
glm::vec3 d = q.pos - p.pos; // distance
float r2 = glm::dot(d,d); // distance squared
float r3 = r2 * glm::sqrt(r2);
float f_mag = (G*p.size*q.size) / (r3 + ETA);
glm::vec3 f = d * f_mag; // force vector
p.acc += f;
q.acc -= f;
numForceCalcs++;
}
}
}
|
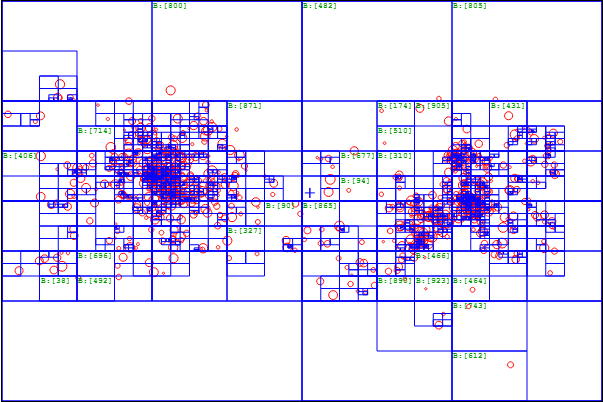
However for larger number of particles this will be exponentially too many calculations for most current computers. An alternative algorithm for approximating these forces is the Barnes Hut Algorithm, where we subdivide the space into an oct-tree, summing of the center of masses of particles in each cell. Then when calculating forces affecting a cell, if a cell is far enough away, we just use the cell mass and centroid instead of calculating for each particle within the cell.
This allows for O(nlogn) computations. In one example with around 10,000 bodies in 2D, we only need 383 thousand force calculations versus the 10 million (10,000^2) calculations of brute force.
Here is an example of subdividing the space in 2D:
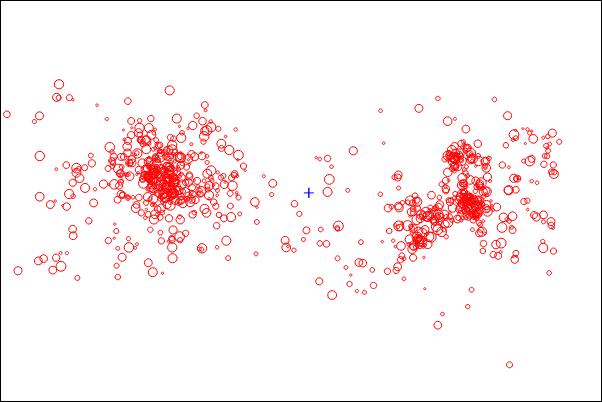 |
| N bodies (size of circle is a function of mass) |
For reference, I previously wrote an
HTML5/Javascript based Barnes Hut N-body simulation which shows the speedup in real-time.