Building a PID hover controller for Kerbal Space Program with kOS and IPython Notebook
Kerbal Space Program is a game that lets you build rockets and launch (explode) them to space into orbits, land (crash) on other planets, and lots of other sorts of fun (disasters). It does a really good job of making learning orbital mechanics a fun experience. The other thing, what this post is about, is that there are a lot of really interesting mods for it, one of which is kOS, a mod that allows you to program your rockets using a simplified scripting language.
So we're going to try and write a kOS script for Kerbal Space Program (KSP) to control a single-stage rocket engine and have it hover at a set altitude. Our intrepid little spaceship consists of a single engine, some landing legs and a parachute in case (when) our controller goes haywire.
There were failures, but we eventually succeeded. Here is the nicer formatted IPython Notebook.
kOS enhances sensors such as an accelerometer, barometer and an avionics hub, to allow the onboard flight computer to track the altitude, airspeed and g-forces of the craft. Using this data we can then write a script to control the thrust of the rocket, and try to make it reach and stay at a goal altitude. For simplicity we use a pre-existing controller for maintaining a vertical orientation (this end must point up or you will not go to space today).
An example kOS script that logs data looks like this:
What is dthrott? Well, we're going to implement, you guessed it, a PID controller. As a first step for hovering, we'll have our controller change in velocity by limiting our g_force to 0 via gforcegoal=1.0.
Where ∥ameasured∥ is our measured current max acceleration using an onboard accelerometer and gmeasured is our onboard gravitational acceleration magnitude using our graviola detector (graviola, what a word).
And in the running controller loop, we update thrott=thrott+Δthrott in kOS as
The onboard computer text file is also saved in our real life computer, so lets go ahead and look at the data with an IPython notebook.
Instead of controlling the rate of change of throttle alone, let's figure out how to find our throttle set-point for hovering directly (throtthover), and then set thrott=throtthover+Δthrott
We know our ship's current max thrust with 100%, which we will call Thrustavailable. What we want to find is our Throttle% which would be
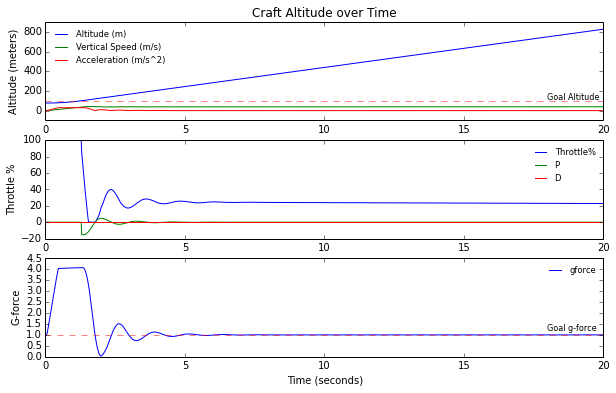
All of this put together, and after twiddling with our PID gains we get our results
Woohoo! It overshoots a little but stablizes smoothly at 100m! Great to see this going in the game, looks a bit like the SpaceX grasshopper.
The kOS script used is hover4.ks and these tests are run by calling RUN hover4(hoverN.txt,20,Kp,Kd)
Source Code on GitHub
So we're going to try and write a kOS script for Kerbal Space Program (KSP) to control a single-stage rocket engine and have it hover at a set altitude. Our intrepid little spaceship consists of a single engine, some landing legs and a parachute in case (when) our controller goes haywire.
There were failures, but we eventually succeeded. Here is the nicer formatted IPython Notebook.
 |
| PID Controlled Hovering KSP rocket - Link to IPython Notebook |
An example kOS script that logs data looks like this:
UNTIL SHIP:LIQUIDFUEL < 0.1 {This says: Until the fuel goes below 0.1 kg (about zero), print out the current g_forces and change in throttle level (to an onboard text file), then update our thrust level based on this dthrott change in throttle, finally wait 0.1 seconds before repeating.
PRINT gforce + " " + dthrott.
SET thrott to thrott + dthrott.
WAIT 0.1.
}
What is dthrott? Well, we're going to implement, you guessed it, a PID controller. As a first step for hovering, we'll have our controller change in velocity by limiting our g_force to 0 via gforcegoal=1.0.
gforceΔthrottthrott=∥a∥/g⟹gforcemeasured=∥ameasured∥/gmeasured=Kp(gforcegoal−gforcemeasured)=Kp(1.0−gforcemeasured)=thrott+Δthrott
Where ∥ameasured∥ is our measured current max acceleration using an onboard accelerometer and gmeasured is our onboard gravitational acceleration magnitude using our graviola detector (graviola, what a word).
Note: I'm still working out a way to make math and code look nice with blogger, so it's not the easiest to read here. Check out the nicer formatted IPython Notebook on github for a better experience.
And in the running controller loop, we update thrott=thrott+Δthrott in kOS as
SET thrott to thrott + dthrott.Where thrott is the throttle percentage from 0 to 1 or no thrust to full thrust. This has the effect of trying to move gforce to 1.0, matching the gravitational force.
The onboard computer text file is also saved in our real life computer, so lets go ahead and look at the data with an IPython notebook.
| %matplotlib inline import matplotlib.pyplot as plt | |
| import numpy as np | |
| from numpy import genfromtxt | |
| from matplotlib.font_manager import FontProperties | |
| from pylab import rcParams | |
| fontP = FontProperties() | |
| fontP.set_size('small') | |
| def loadData(filename): | |
| return genfromtxt(filename, delimiter=' ') | |
| def plotData(data): | |
| rcParams['figure.figsize'] = 10, 6 # Set figure size to 10" wide x 6" tall | |
| t = data[:,0] | |
| altitude = data[:,1] | |
| verticalspeed = data[:,2] | |
| acceleration = data[:,3] # magnitude of acceleration | |
| gforce = data[:,4] | |
| throttle = data[:,5] * 100 | |
| dthrottle_p = data[:,6] * 100 | |
| dthrottle_d = data[:,7] * 100 | |
| # Top subplot, position and velocity up to threshold | |
| plt.subplot(3, 1, 1) | |
| plt.plot(t, altitude, t, verticalspeed, t, acceleration) | |
| plt.axhline(y=100,linewidth=1,alpha=0.5,color='r',linestyle='--',label='goal'); | |
| plt.text(max(t)*0.9, 105, 'Goal Altitude', fontsize=8); | |
| plt.title('Craft Altitude over Time') | |
| plt.ylabel('Altitude (meters)') | |
| plt.legend(['Altitude (m)','Vertical Speed (m/s)', 'Acceleration (m/s^2)'], "best", prop=fontP, frameon=False) | |
| # Middle subplot, throttle & dthrottle | |
| plt.subplot(3, 1, 2) | |
| plt.plot(t, throttle, t, dthrottle_p, t, dthrottle_d) | |
| plt.legend(['Throttle%','P','D'], "best", prop=fontP, frameon=False) # Small font, best location | |
| plt.ylabel('Throttle %') | |
| # Bottom subplot, gforce | |
| plt.subplot(3, 1, 3) | |
| plt.plot(t, gforce) | |
| plt.axhline(y=1,linewidth=1,alpha=0.5,color='r',linestyle='--',label='goal'); | |
| plt.text(max(t)*0.9, 1.2, 'Goal g-force', fontsize=8); | |
| plt.legend(['gforce'], "best", bbox_to_anchor=(1.0, 1.0), prop=fontP, frameon = False) # Small font, best location | |
| plt.xlabel('Time (seconds)') | |
| plt.ylabel('G-force'); | |
| plt.show(); |
G-force Control
As a first test, we'll start from the launchpad, thrust at full throttle till we hit altitudegoal>100 meters and then use a proportional gain of Kp=0.05 to keep gforce∼1.0.LOCK dthrott_p TO Kp * (1.0 - gforce).
LOCK dthrott TO dthrott_p.
And then we can plot it in our notebook with:
Pretty cool! Once it passes 100m altitude the controller starts, the throttle controls for gforce, bringing it oscillating down around 1g. This zeros our acceleration but not our existing velocity, so the position continues to increase. We could add some derivative gain to damp down the gforce overshoot, but it won't solve this problem yet.
The kOS script to run this test is located in hover1.ks and called on gforce.txt by RUN hover1(gforce.txt,20)
data = loadData('collected_data\\gforce.txt')
plotData(data)
 |
| G-force based hover controller |
The kOS script to run this test is located in hover1.ks and called on gforce.txt by RUN hover1(gforce.txt,20)
Hover set-point
Instead of controlling the rate of change of throttle alone, let's figure out how to find our throttle set-point for hovering directly (throtthover), and then set thrott=throtthover+Δthrott
We know our ship's current max thrust with 100%, which we will call Thrustavailable. What we want to find is our Throttle% which would be
Throttle%=Thrustdesired / ThrustavailableWhere Throttle% is between 0 and 1 (0 - 100%). Our Thrustdesired is when we have a thrust to weight ratio of 1, matching gravitational acceleration.
TWR=F/mg=1
Fthrust=mg
g=μplanet / (PLANET:RADIUS)^2
Thrustdesired=SHIP:MASS∗g
Finally that gives us
Throttle%=( SHIP:MASS∗μplanet / (PLANET:RADIUS)^2 ) / Thrustavailable
And in kOS it is
LOCK hover_throttle_level TO MIN(1, MAX(0, SHIP:MASS * g / MAX(0.0001, curr_engine:AVAILABLETHRUST))).
All of this put together, and after twiddling with our PID gains we get our results
 |
| KSP Rocket hovering at a set-point of 100m |
The kOS script used is hover4.ks and these tests are run by calling RUN hover4(hoverN.txt,20,Kp,Kd)
Source Code on GitHub

